Peter Medhurst

Unfortunately, my parents were not great cinema goers when I was a child, so I didn’t get a chance to see The Sound of Music until its 10th anniverary in 1975 when a flurry of screenings took place up and down the country. I remember that I managed to catch up with the film in Plymouth and by one of those extraordinary twists of fate, the person who sat immediately on my right in the stalls was Agatha Christie, but that’s a story for another occasion . . . .

At the time, I was coming to the end of my second year at the Royal College of Music and therefore knew everything there was to know about music. And among my many unshakeable beliefs was the certainty that the film I was about to see could hold nothing for me musically.  Oh dear, the conceit of youth . . . . .

Even before the opening credits had finished I became an instant Sound of Music tart and knew that I was destined to worship at the feet of Richard Rodgers for ever. It would embarass me hugely to have to tell you how many times over the years I’ve seen that film.

No matter, I adored The Lonely Goatherd song – I do to this day – with its wonderful display of counterpoint heard at the moment when all the puppets dance together; I loved Climb Every Mountain which contains ingenius modulations that are almost worthy of Schubert; but it was when Maria on that mountainside taught the von Trapp children to sing Doe, a Deer, a Female Deer that something clicked in my imagination regarding the scale. I remember thinking how powerful were these fundamental building blocks of music and that the simple scale had an allure and fascination all of its own.

Scales in Berlioz’s Fantastic Symphony

For example, a few years before that I’d come across Berlioz’s Fantastic Symphony of 1830 and of all passages in the score to capture my attention was the closing section of the 2nd movement, the scene at the ball. You’ll remember that at this point the whole orchestra is going full pelt and has the double bar clearly in its sightline, when quite unexpectedly out of the rush of exuberant notes emerge two glorious descending major scales, thus (it begins in bar 8):

When I heard that passage for the first time, I marvelled at Berlioz’s boldness in bringing into play something so elemental as a diatonic scale (a scale without accidentals), a musical device one usually associates with the practice room or schoolroom, rather than the concert hall.  However, the composer pulls the extravagant moment off magnificently and that particular passage becomes – at least to my mind – one of the highlights of the work.  To this day I look forward to its arrival whenever I listen to the Symphony and it never fails in delighting me.

At around the same time, but in another area of music, I discovered Vivaldi’s Op 10 set of flute concertos, published c1728.  In the first movement of Concerto in F Op 10 No 1, Vivaldi goes a step farther than Berlioz and utilises scales as a driving force behind the entire movement.  Notice how the scales of F major and C major dominate the first four bars of the opening ritornello, which in turn inspire descending scales in the bars that follow (below).  However, unlike Berlioz, I think there really is a whiff of the schoolroom about the music.  Vivaldi almost certainly wrote the Op 10 concertos for his young students at the Ospedale della Pietà in Venice, yet while he incorporates scalic exercises into the body of the movement, the music is nonetheless extraordinarily inventive and musically powerful.

Where does the Western scale come from?

At any rate, back to The Sound of Music.  After seeing the film, I realised that I knew almost nothing about the Western scale other than the fact that it existed.  I knew about major and minor scales, of course, having practiced them tirelessly for my Grade VIII piano, and I also knew a little about modes, but beyond that I was in the dark. So, I fell to thinking: Where did the scale come from? How long had it been around? Who invented it? Was it Medieval, Roman, Greek or Egyptian? I set about trying to find out. And it has led me down a path of discovery that has influenced the way in which I view – on which I still am walking – in the continual search . . . . . .  power of the scale: Doh Re Me Far Soh La Tee

At this point I could go on for pages and pages listing various eminant scholars’ very persuasive views on the genesis of the scale, but for your sake and mine, it’s probably best to summerise all the ideas, because for the moment I’m actually more interested in the physics and the mathematics of the scale, rather than its illusive beginnings.  Essentially the theories boil down to this: its claimed that the componants of our Western scale can be traced back to the Ancient Greeks and particularly to Pythagoras in the 6th century B.C. Many claim that the mathematician, Pythagoras invented the scale due to his experiments in the 6th century.  However others claim that the scale was around and in use long before that and that it might go right back to the beginning of human history. I must say, I’m inclined to believe that that is the case. Perhaps what we should say is that Pythagoras qualified the scale by understanding the mathematical relationship between the seven notes of the scale.

Pythagoras

Pythagoras was a 6th century B.C. philosopher and mathematician and is said to have died at the age of 75 roundabout 495 B.C. Interestingly, no actual writings survive by him – if ever there were any – but his ideas and teachings were handed on by word of mouth and written about and interpreted by Plato and his followers some 150 years later.  There’s a famous legend telling how one day, as Paythagoras was passing a blacksmith premises, he heard the most glorious sounds emanating from the workshop.  Astonished, he rushed inside to see what was producing the heavenly sound, only to discover four blacksmiths hammering away and shaping pieces of metal on their anvils.

Pythagoras noticed that the anvils were of different sizes and in arithmetical proportions to one another:

there was a large one

one that was ½ its size

one that was a ⅓ of its size

and another  that was a ¼ of its size

and together they made an extraordinary music (harmony) when struck by the smithies.  I have a feeling that the story has nothing to do with anvils at all, but everything to do with vibrating strings.

The monochord

Let’s pause here for a moment and remind ourselves about an early instrument well known to Pythagorus: the ‘monochord’ and here it is:

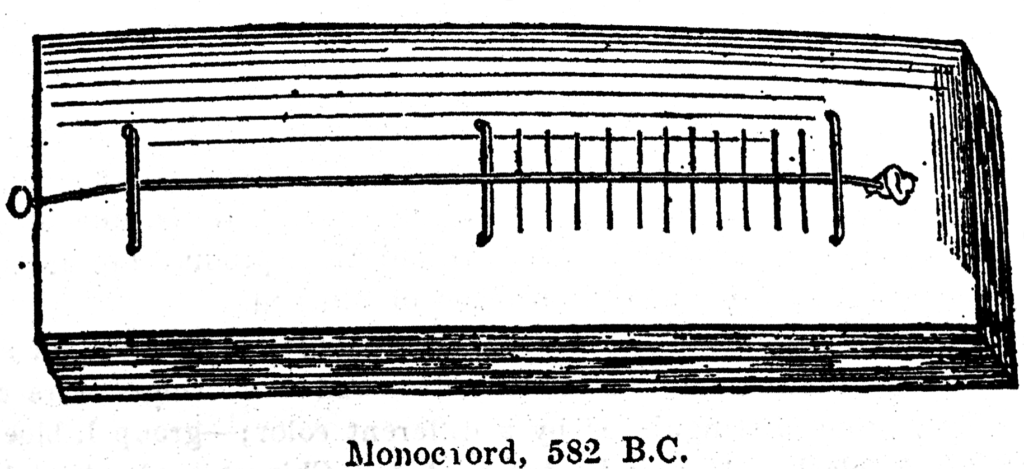
The monochord consists of a metal string stretched over a hollow resonating body. Using a movable bridge, the string can be divided into two portions whose lengths may be set at any ratio to give various pitches and musical intervals when plucked or struck.  “With its single string, movable bridge and graduated rule, the monochord straddled the gap between notes and numbers, intervals and ratios, sense-perception and mathematical reason.” wrote Dr Crotch in 1861 in an essay “On the Derivation of the Scale, Tuning, Temperament, the Monochord, etc.” in The Musical Times.

I don’t think that we’ll ever know who invented the monochord, but it is an instrument most closely associated with Pythagorus and his experiments in musical accoustics;

In fact, in Gafori’s Theorica Musice published in Milan in 1492, Pythagorus is shown experimenting with a very sophisticated monochord, showing all the principal features of the instrument: strings, bridges, hitchpins, weights, and hammers, or pluckers.

Strings, bridges, hitchpins, weights, and hammers, or pluckers, are of course the common features of the piano, the harpsichord, the guitar, the violin, the harp, the lute, the mandolin, the dulcimer, etc

The monochord is the essence of these intruments.

What pythagorus discovered on his monochord was this:

If you halve a vibrating string at exactly the midway point, creating a ratio of 2:1, then the note that emerges is exactly an octave – irrespective of the length of the string.

To you and me that means 8 notes above the first note of the scale, in other words: doh.

i) The most important note is the fundamental – Note 1 of the scale – TONIC
ii) The next is note 5, 5th – Dominant note
iii) The next is note 4, 4th – Subdominant

These notes and their relationships – and their implied harmonic relationships – underpin western music right the way through to the early 20th century. There influence is only challenged with the arrival of the composer Arnold Schönberg and his movement towards atonalism between 1900 and 1910.

Any tune can be harmonised by I, V, & IV

Do you remember that 1968 film, 2001: A Space Odyssey?

Rather like the film The Girl with the Pearl Ear Ring nothing of any consequence seems to happen over the space of 2 hours, but none the less you know that you are watching a ground breaking piece of cinema.

Well, the music that was used to accompany the opening credits to the film was the opening of Richard Strauss’ Also Sprach Zarathustra – written in 1896 and inspired by Friedrich Nietzsche’s philosophical novel of the same name.

Let’s hear it and remind ourselves of it – you’ll all know it Press for Music

Also sprach Zarathustra is a tone poem and typically lasts half an hour in performance. The bit, however, that we are interested in is the magnificent opening.

And this opening, or fanfare – entitled “Sunrise” in the composer’s original programme notes, was thought to evoke just the right mood for Stanley Kubrick’s 2001: A Space Odyssey film.

Music is “timeless” in feel

Strauss uses: Notes 1, 5, 4, and 3, and their implied harmonies.

Did you do this as a child? Blow across the top of a bottle to produce a note?

The Harmonic series
Every note that you hear, or play, is made up of more than 1 note. There is 1 note that dominates the sound – it is the lowest one, and we call it the fundamental.

We can plot these notes – these harmonics – and in ascending order they are:

C C G C E G etc

Reveal the harmonics

Pythagorus and his followers always claimed that the notes that sound well together in harmony are those that have strong mathematical relationships to one another, but you and I have seen that they are also the first notes of the harmonic series.

So, it comes as no surprise to me that the very first known and surviving attempts at harmony in church music approximately 880 AD – in the dark ages the church was the nurturer of culture, including music that they used for liturgy, – should have favoured harmony inspired by the octave, 5th and 4th

Again, I’m going to pause for a moment, and answer a question that may be forming at this moment in your minds:

The theory is all very well, but is it music? Did the Greeks recognise the emotional nature of music?

The short answers are: Yes, it is music, and yes the Ancients recognised the emotional nature of music, and the consequent power it possessed.

We hear emotion in the music of later times

But so did the Greeks

1. Guido of Arezzo – Italian music theorist of the Medieval era. He is regarded as the inventor of modern musical notation d.1090
2. Adam of Fulda (c. 1445 – 1505)[1] was a German musical author of the second half of the 15th century. He was born in Fulda and died in Wittenberg.
3. Juan de Espinosa Medrano (ca. 1629 -1688), was a Peruvian cleric, preacher, author of philosophical and literary tracts

Modes – Dorian = D, Phrygian = E, Lydian = F, Mixolydian = G

Keys

Qualities of Cm, G major

This is what Grove’s Dictionary of Music and Musicians says:

[A scale is a] sequence of notes in ascending or descending order of pitch. As a musicological concept, a scale is a sequence long enough to define unambiguously a mode, tonality, or some special linear construction, and that begins and ends (where appropriate) on the fundamental note of the tonality or mode; a scale, therefore, is usually thought of as having the compass of one or more octaves. The following discussion is limited to the scales of European musical theory.

Seven-note scales lying within the octave, which are also known as ‘heptachords’, contain one representative of each letter name (A–B–C–D–E–F–G), any of which may be inflected by an accidental. A scale is Diatonic if the sequence of notes is based on a particular species of octave consisting of five tones (t) and two semitones (s). The white notes of the piano perhaps offer the simplest illustration of diatonic scales; see Table 1. The scales on D, E, F and G as given are the most common of the four authentic church modes (see Mode). The Locrian or Hyperaeolian scale, given on B in Table 1, is almost never used, since the unstable interval of a tritone occurs between the two most important degrees, the first and fifth. The remaining scales are those of the major and minor mode without any key signature.